📝Category Theory: Product

tags: § Category Theory

\begin{tikzcd} & X \arrow[ld, "f_1", swap] \arrow[d, "f", dashed] \arrow[rd, "f_2"] & \\ A & P \arrow[l, "\pi_1"] \arrow[r, "\pi_2", swap] & B \end{tikzcd}

Universal construction:

$P, \pi_1, \pi_2$ is the (categorical) product of $A$ and $B$ if $\pi_1 : P \to A$ and $\pi_2 : P \to B$ and $\forall(X, f_1 : X \to A, f_2 : X \to B)\; \exists! f : X \to P \ni \pi_1 \circ f = f_1, \pi_2 \circ f = f_2$

Also:

$P$ is usually called $A\times B$ or in types: $(A,B)$
$\pi_1$ and $\pi_2$ are called projections.

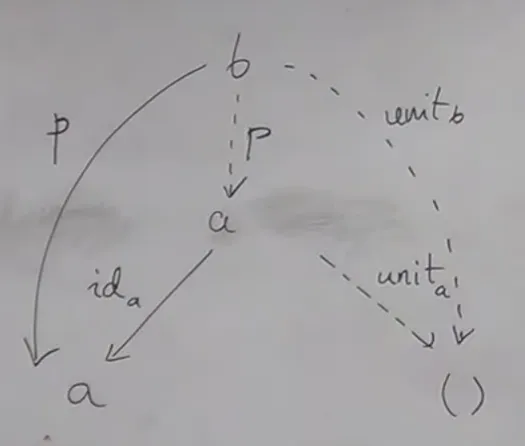
Terminal object is a unit value of categorical product ( $a\times() \cong a$ ) (forming a Monoid and Cartesian monoidal category).

Backlinks

📝 Category Theory: Coproduct
📝 Cartesian monoidal category
📝 § Category Theory