📝Binary relation properties

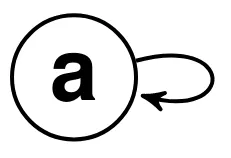
Reflexive:

• for every x, x ≤ x

• as a graph:

  

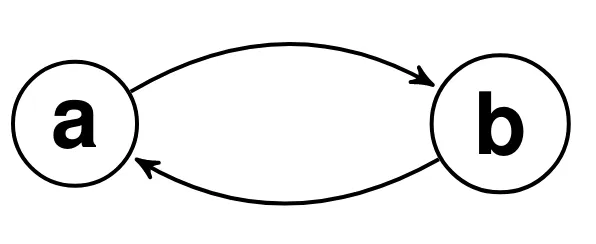
Symmetric:

• For every x and y, if x ≤ y then y ≤ x
• if there is an edge between vertices, there is an edge in the opposite direction

• as a graph

  

Antisymmetric:

• If x ≤ y and y ≤ x, then x = y
• if there is an edge between vertices, there is no other edge in the opposite direction

• as a graph:

  \begin{tikzcd} a \arrow[loop left] \arrow[r] & b \end{tikzcd}

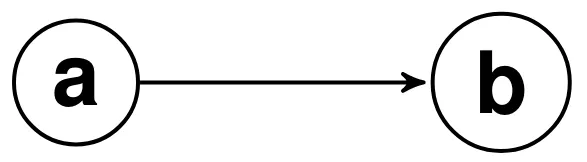
Asymmetric:

• $\forall a,b \in X : a R b \rightarrow \lnot (b R a)$ (including $a=b$)
• A relation is asymmetric iff it is both antisymmetric and irreflexive

• as a graph:

  

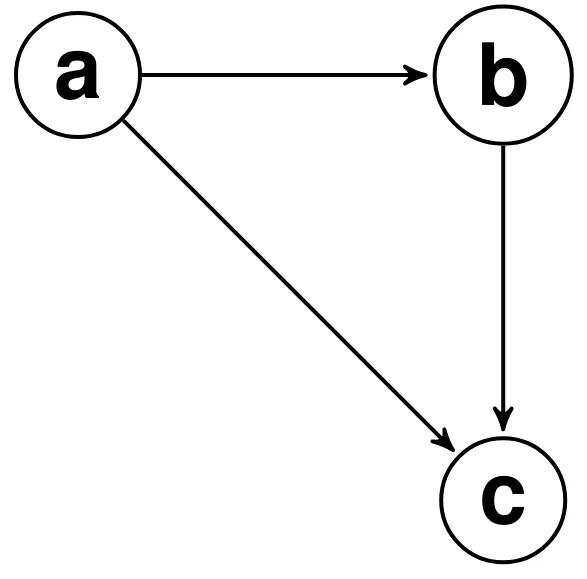
Transitive:

• If x ≤ y and y ≤ z, then x ≤ z

• as a graph:

  

Connexity (connex relation):

• the relation is defined between all pairs of elements
• $\forall x, y \in X, x R y \lor y R x$

Semiconnexity (semiconnex relation):

• the relation is defined between all pairs of distinct elements
• $\forall x, y \in X, x \ne y \rightarrow x R y \lor y R x$