📖Category Theory for Programmers

August 13, 2020. Last modified: May 24, 2021

authors: Milewski, Bartosz
year: 2016
url: https://www.youtube.com/playlist?list=PLbgaMIhjbmEnaH_LTkxLI7FMa2HsnawM_

1.1 Motivation and Philosophy

Category Theory 1.1: Motivation and Philosophy

Curry–Howard–Lambek correspondence
- Computation–Logic–Category theory are isomorphic
OOP is bad for concurrent programming because OOP hides data mutation and sharing (pointers). Mixing sharing and mutation is data race.
- this makes objects non-composable
- locks do not compose either
Template metaprogramming in C++ draws many ideas from Haskell. So you translate Haskell ideas into ugly C++ metaprogramming language.
- Haskell draws many ideas from Category Theory. So you translate concise Category Theory ideas into ugly Haskell language.
Category Theory unifies different branches of mathematics: type theory, logic, algebra, etc.
- Mathematics get philosophical: do mathematicians invent things or discover truth?
It might be that composition and this universal structure is not the property of the universe, but the property of human minds.
- It might be that humans evolved to work with abstraction and composition, and we don’t understand what we can’t explore using these tools.
- In that sense, Category Theory might be about human minds really and be closer to epistemology.

1.2 What is a category?

Category Theory 1.2: What is a category?

Category

7.1: Functoriality, bifunctors

Functors consist of functions and functions compose, so we can compose functors
Identity functor is trivial
Cat = Category of functors
- Objects are categories
- Morphisms are functors
- It’s a category of small categories. For large categories, we need a more powerful mechanisms
(Now, Haskell does not really allow composition of functors. If you have a Maybe [Int] (composition of two functors: Maybe and []), you have to use two fmaps instead of one.)
all algebraic data types are automatically functorial
bifunctor — is a functor from a product category (C×D → E)
- sum type is bifunctor as well

7.2: Monoidal Categories, Functoriality of ADTs, Profunctors

(cartesian) product (operator) + terminal object (Void) (a unit) is a monoidal category
- terminal object is a unit of product
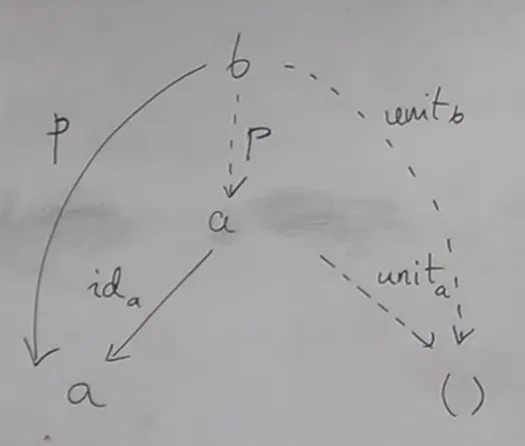
by the same token, coproduct + initial object is a monoidal category
a monoidal category (or tensor category)
- a bifunctor: $\otimes: C \times C \to C$ $\otimes : C \times C \to C$ called a tensor product
  - (e.g., product or coproduct)
- an object $I$ or $1$ called the unit object or identity object.
Contravariant functor — is a functor defined on the opposite category (cofunctor? no)
- haskelly-speaking
```
class Contravariant f where
  contramap :: (a -> b) -> f b -> f a
  -- must satisfy:
  -- contramap id = id
  -- contramap f . contramap g = contramap (g . f)
```
- (Strictly speaking, “cofunctor” is not the right name as the dual of a functor is a functor)
- you can think of Contravariant as an opposite of container. it does not contain As, but it requires As
function
- (->) a b is Contravariant in a and Covariant in b
- $C^{op} \times C \to C$ $C^{o p} \times C \to C$
  - that is called a Profunctor
- haskell
```
class Profunctor p where
  dimap :: (a' -> a) -> (b -> b') -> p a b -> p a' b'

instance Profunctor (->) where
  -- dimap :: (a' -> a) -> (b -> b') -> (a -> b) -> (a' -> b')
  dimap f g h = g . h . f
```
- (how does that definition match to the Profunctor definition on wikipedia or nLab? $\phi: C \nrightarrow D \equiv \phi: D^{op}\times{}C \to Set$ )

8.1: Function objects, exponentials

hom-set between two objects (if it’s a set), can be represented as an object in the same category
- “internal hom-set”
function objects:
- pattern
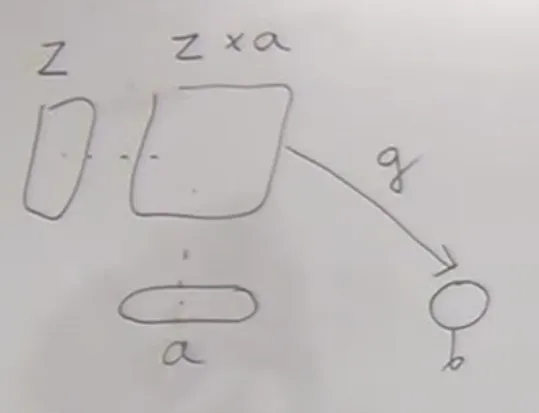
  - z is a function, a is an argument type, b—result type
  - the category must have products
- universal construction
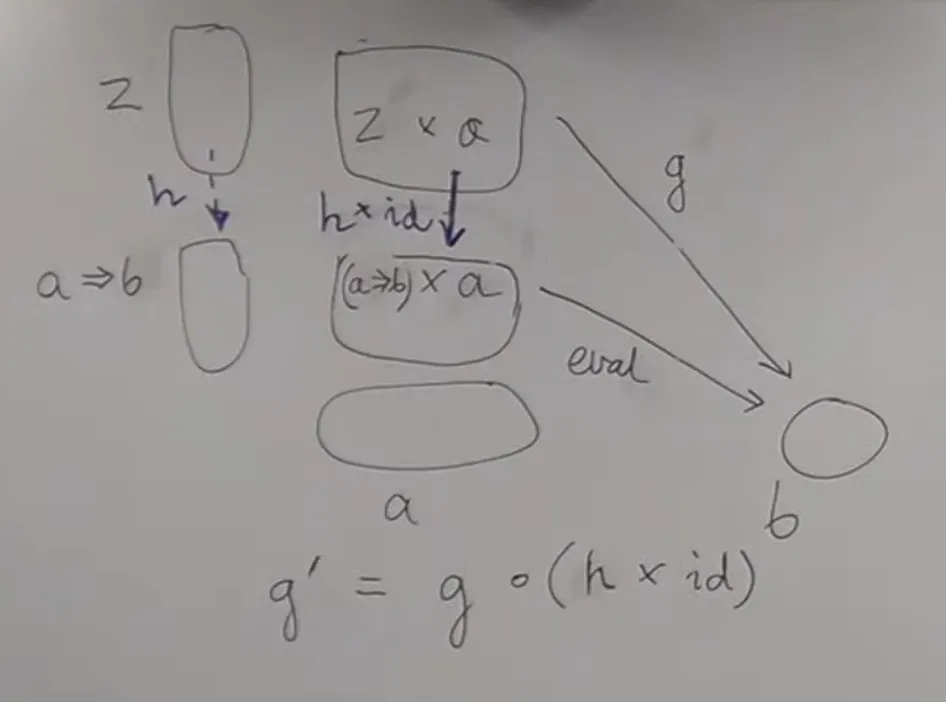
  - $\var{a \Rightarrow b} \text{ is a function object} \iff \forall z, \exists! h: z \to (a \Rightarrow b) \ni g = \var{eval} \circ (h \times id)$ $\vara⇒b is a function object⟺∀z,∃!h:z→(a⇒b)∋g=\vareval∘(h×id)$
    - (this relies on that a morphism between two products can be constructed as a product of two morphisms ( $h$ and $id$ here), and we know that that is a correct way to obtain $(a \Rightarrow b) \times a$ from $z \times a$ using $h: z \to (a \Rightarrow b)$ )
  - in haskell, the next two are equivalent
```
h :: z -> (a -> b)
g :: (z, a) -> b
```
    (currying)
```
curry :: ((a, b) -> c) -> (a -> (b -> c))
curry f = \a -> \b -> f (a, b)

uncurry :: (a -> (b -> c)) -> ((a, b) -> c)
uncurry f = \(a, b) -> f a b
```
exponentials
- $a \Rightarrow b \equiv b^a$
- e.g., $Bool \to Int \equiv (Int, Int) \equiv Int \times Int \equiv Int^2 \equiv Int^{Bool}$ $B oo l \to I n t \equiv (I n t, I n t) \equiv I n t \times I n t \equiv I n t^{2} \equiv I n t^{B oo l}$
  - $1 = ()$
  - $2 = Bool$
- cartesian closed category (CCC)
  - cartesian — has products
  - closed — has all exponentials $\forall{}a,b, \exists{}a^b$ $\forall a, b, \exists a^{b}$
    - A category $C$ is closed if for any pair $a,b$ of objects the collection of morphisms from $a$ to $b$ can be regarded as forming itself an object of $C$ .
  - has a terminal object (0th power of an object)
- Bicartesian closed category (BCCC)
  - has products, co-products, exponentials, and initial and terminal objects
  - bicartesian = both cartesian and cocartesian
- $a^0 = 1 \implies Void \to a \sim ()$ (absurd)
- $1^a = 1 \implies a \to () \sim ()$
- $a^1 = a \implies () \to a \sim a$

8.2 Type algebra, Curry-Howard-Lambek isomorphism

$a^{b+c} = a^b \times a^c$

Backlinks

📝 § Category Theory